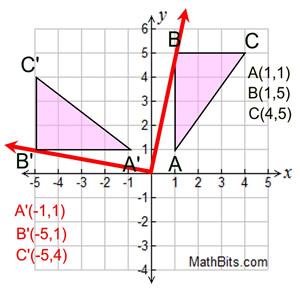
A transformation in which a plane figure turns around a fixed center point. In other words, one point on the plane, the center of rotation, is fixed and everything else on the plane rotates about that point by a given angle.
A way to make rotations easier to graph is by using coordinate notation.
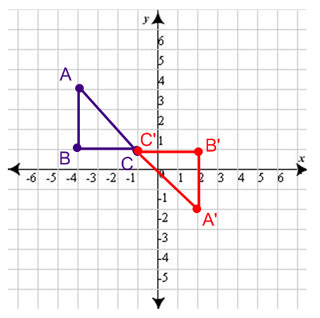
To graph the rotation 90 degrees clockwise about the origin, use the formula (x,y)→(y,-x)
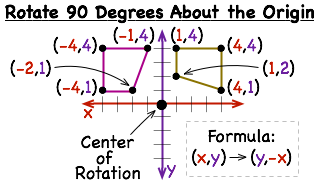
To graph the rotation 90 degrees counterclockwise about the origin, use the formula (x,y)→(-y,x)

To graph a rotation 180 degrees in either direction around the origin, use the formula (x,y)→(-x,-y)
A translation simply means moving without rotating, resizing or anything else, just moving.
To graph a translation use the formula (x,y)→(x+a,y+b). the a represents the change in the x axis and the b represents the change in the y axis.
A reflection is a flip over a line. Every point is the same size as the orginal image, and every point is the same distance form the central line.
The central line is called the mirror line.
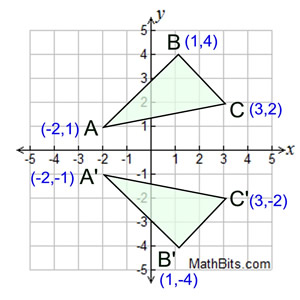
To graph a reflection over the x-axis, use the formula (x,y)→(x,-y)
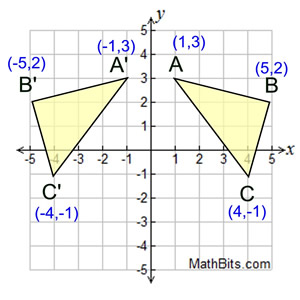
To graph a reflection over the y-axis, use the formula (x,y)→(-x,y)
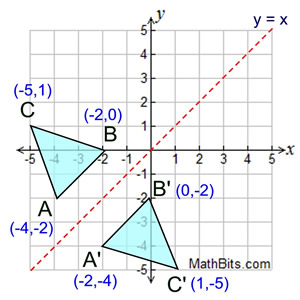
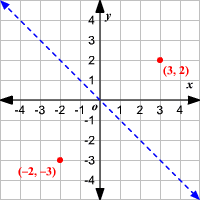
To graph a reflection across the line y=x, the formula is (x,y)→(y,x)
To graph a reflection across the line y=-x, the formula is (x,y)→(-y,-x)
The MOST IMPORTANT rule to remember for the regents is when they ask you if any of these transformations are congruent, write "A reflection/translation/rotation is a basic rigid motion, therefore distance is preserved."
Click Here for the practice questions on rigid motions.